memalign.github.io
( ( ( featured projects ) ) )
( ( ( posts ) ) )
Catch Tap Toy
MemSky
Create Your Own Wolfer
Wolfers
Phonics Flashcards
Mandarin Flashcards
Mandarin Communication Board
Counting Tap Toy
Space Trader
MemPlayer
Slice Tap Toy
CaveRibbon
Octogram
Mastodon API
AirDesk
FreshRSS
Fireworks Tap Toy
Remember Forgotten Names
Emscripten on Raspberry Pi 400
Simplify Picking a Restaurant
Trippy Art
Tap Toy
MemSky
Create Your Own Wolfer
Wolfers
Phonics Flashcards
Mandarin Flashcards
Mandarin Communication Board
Counting Tap Toy
Space Trader
MemPlayer
Slice Tap Toy
CaveRibbon
Octogram
Mastodon API
AirDesk
FreshRSS
Fireworks Tap Toy
Remember Forgotten Names
Emscripten on Raspberry Pi 400
Simplify Picking a Restaurant
Trippy Art
Tap Toy
PCEImage Editor
PCEImage
My Beatles Picks
SoundsJustLike
PuzzleScript
Wheat Chex
PICO-8
Fussy Baby Checklist
Fall Asleep
Shape Your Destiny
Tim's Vermeer
Day and Night
Lights Off
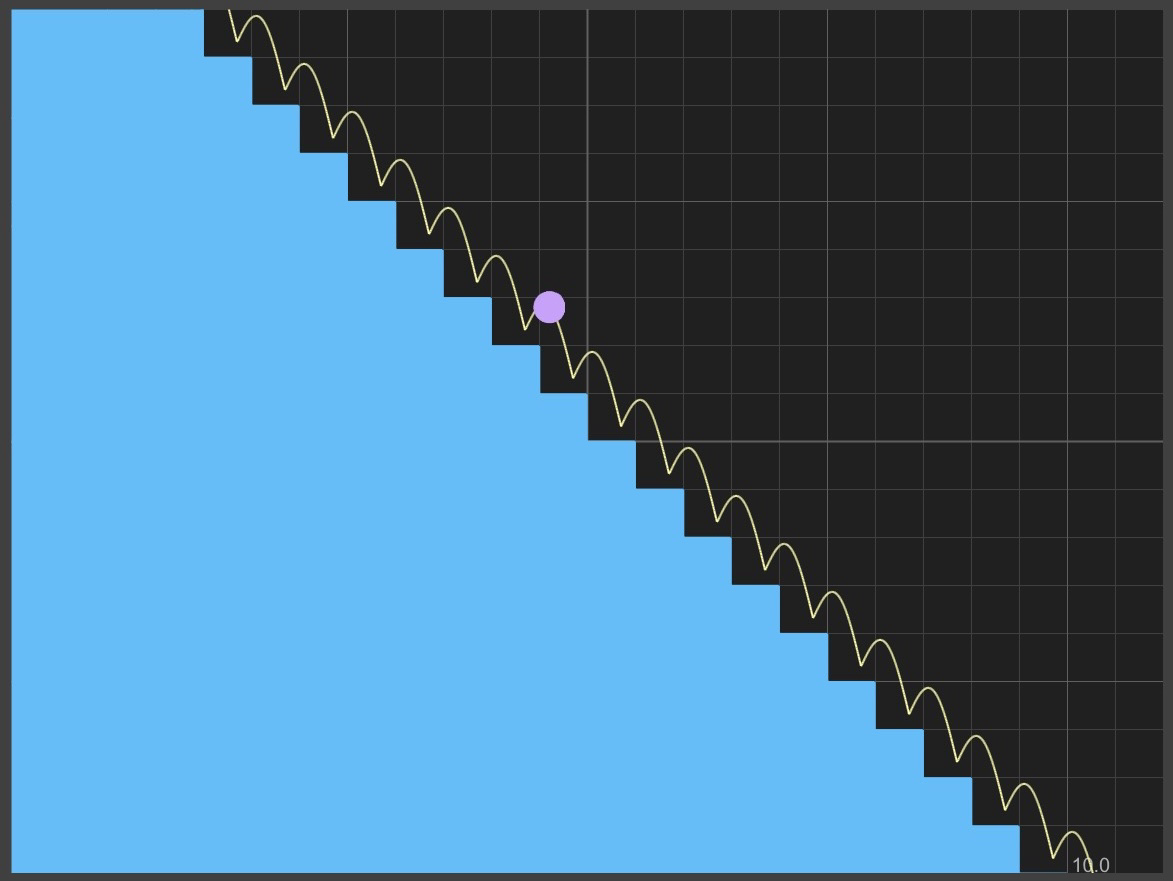
Batman Curve
FormulaGraph
Bouncing Ball
Catalog of Math Shapes
Draw Shapes Using Math
Similar Songs
Building a Reddit app
Counterfeit Monkey
Listed Action Interactive Fiction
PCEImage
My Beatles Picks
SoundsJustLike
PuzzleScript
Wheat Chex
PICO-8
Fussy Baby Checklist
Fall Asleep
Shape Your Destiny
Tim's Vermeer
Day and Night
Lights Off
Batman Curve
FormulaGraph
Bouncing Ball
Catalog of Math Shapes
Draw Shapes Using Math
Similar Songs
Building a Reddit app
Counterfeit Monkey
Listed Action Interactive Fiction
Andrew Plotkin's Zarfhome
Product Review Writing Prompts
Dungeon Memalign
Pac-Man Dungeon
The Queen's Gambit
Rebecca Meyer
Coding Machines
Clamps
Emoji Simulator
Universal Paperclips
Fall Down the Rabbit Hole
Live COVID-19 Dashboard
Create COVID-19 Graphs Using JavaScript
Books
notes.txt
Download Video Into Your Brain
Download Text Into Your Brain
Source Control
Personal Projects
How to Program a Text Adventure
RSS and Feedly
Welcome
Product Review Writing Prompts
Dungeon Memalign
Pac-Man Dungeon
The Queen's Gambit
Rebecca Meyer
Coding Machines
Clamps
Emoji Simulator
Universal Paperclips
Fall Down the Rabbit Hole
Live COVID-19 Dashboard
Create COVID-19 Graphs Using JavaScript
Books
notes.txt
Download Video Into Your Brain
Download Text Into Your Brain
Source Control
Personal Projects
How to Program a Text Adventure
RSS and Feedly
Welcome
 Introducing Catch Tap Toy, the latest addition to the Tap Toy series.
Introducing Catch Tap Toy, the latest addition to the Tap Toy series.(See also: Counting Tap Toy, Slice Tap Toy, Fireworks Tap Toy, Tap Toy)
You can play it in the browser or add it to your home screen as a progressive web app.
I used royalty free game assets from Kenney. That site is awesome thanks to its broad selection of high quality game art.
I also used royalty free music. Credit:
Cyber Crime Story by | e s c p | https://www.escp.space
https://escp-music.bandcamp.com
I built this game to satisfy my nostalgia for one of the first games I ever played on a computer, Walnuts (playable on archive.org), which was apparently published in 1994.https://escp-music.bandcamp.com
The basic gameplay is the same: catch the gems and avoid the spikes. I added a twist: worms you can catch for bonus points.
I recently discovered that this gameplay dates back to Kaboom! (1981) which is itself a clone of Avalanche (1978).
I built this project using Google's Gemini CLI, starting with an old implementation of the game I wrote many years ago in Objective-C.
We're at an interesting phase of AI capability. It's easier than ever to make simple games like this. Is it still worth bothering to make and share something like this?
I think so. I made this for myself and to share with my son. Since I showed him the game first working (I called it a "preview" of a new game I'm making), he has frequently asked to play the "preview" again. That is special.
Also, the choices I make matter. They give this project meaning to myself and maybe also others. I picked the music, the art, and the special twists. Even though the game is simple, there are enough choices to make and options for each choice that nobody else would arrive at the same end result. (I even chose to keep a behavior that could be considered a bug: try playing this game on a phone-sized screen in landscape orientation for an extra amusing challenge) This whole game has been molded and curated for the player's enjoyment.
So I hope you like it!
 Today, I'm sharing a web app for keeping up with your Bluesky timeline: MemSky.
Today, I'm sharing a web app for keeping up with your Bluesky timeline: MemSky.You can use it in the browser or add it to your home screen as a progressive web app.
Everything is local in the web app except for the API calls to Bluesky directly to authenticate and fetch content.
You can browse in two modes:
1. Prioritize Unread Posts (the default) - Keep track of which posts you've already seen and start at the place in the timeline that you left off.
2. Infinite scrolling timeline - Uncheck the Prioritize Unread Posts to use this more standard mode.
In Settings, you can configure Muted Words to filter out any terms you don't care to see.
Why I built this:
I added Bluesky to my collection of news feeds over a year ago. Similar to Mastodon, I found that the official app doesn't do the one thing I want: to read a chronological timeline of posts and reposts from accounts I follow - always keeping my spot since the last time I checked.
For Mastodon, I wrote my own native app to do this in 2023. It's been great, but it's only usable by me. I don't have a developer account to publish native apps.
During the recent winter break, I wondered if a Bluesky client could be built entirely as a web app. I asked ChatGPT to create a one-file web app to see what could be done quickly. It was good enough that I figured I could spend the next week building it into what I want. Why a web app? They work on all platforms and are so easy to share! And LLMs make web apps super fun to whip up regardless of the device you're developing on.
Some technical details:
The hardest part of this project was to load new posts above the posts you have already read. The strategy I landed on: create a snapshot of the page, block user input, load the posts, adjust the scroll offset to pin the posts shown in the snapshot to the exact same position, once scrolling stabilizes remove the snapshot and unblock user input.
Automatic scrolling while pinning elements to the exact same visual position is not well supported by browser APIs. The APIs available let you find the current position of an element in the viewport, but that position needs to be corrected for any change in the viewport size. On iOS, Safari's UI chrome shrinks as a result of scrolling down, so the viewport changes because of the automatic scrolling the web app performs. This was tricky to get right.
 In my post about Wolfers, I mentioned working on a way to generate new game variants.
In my post about Wolfers, I mentioned working on a way to generate new game variants.I'm ready to share that today. Please check out the Create Your Own Wolfer page!
That page is a step-by-step guide to generate your own Wolfer game with only an English description. It also provides a way to load and test your game before submitting it to be included on the official Wolfers page.
I had the best results generating games with ChatGPT, though I provide links to additional AI chat bot choices.
Wolfers games can be educational or just plain fun. Check out this novelty Wolfer game where you have to determine whether a name is a Pokémon or a prescription medication: Wolfer: PokéPrescription.
Some technical details:
- Like PCEImage Editor, I'm using CodeMirror for in-line code editing.
- For user submissions, I'm using a Google Form because it's easy, free, and my projects are just statically hosted files.
 Introducing Wolfers!
Introducing Wolfers!Wolfers is a series of games, playable in your web browser, inspired by the iconic Word Munchers and Number Munchers games of the 1980s/1990s. Wolf down correct answers while avoiding the WoeBots! Take refuge in the Safe Space... if it appears in time!
I've wanted to bring this style of educational game back to life for a long time.
In the early 90s, my grandmother had a Macintosh with educational games. She was a teacher who specialized in teaching reading. She showed me how to play Word Munchers and I had a blast munching words with the right vowel sounds.
Around 2021, I started building a version of this game while on new parent leave from work shortly after my son was born. I returned to work before it was complete and the game was left in stasis.
After that, I got the itch to build many other projects, most of which I've shared here already. These are passion projects. I pursue what interests me the most at any given time, even when that leaves some other project on the backburner. Recently, teaching my son has inspired me to make several apps and this also revived my interest in Wolfers.
These days, I don't have much time or energy for programming because of demanding work and life responsibilities. Yet I still have interest. I still have the itch to build. I also still have a desire to use cutting-edge tools. I decided to give Gemini CLI a try. Google currently offers a fairly generous free tier for Gemini. I ended up impressed. Even though Gemini could be slow, go off-track, and need correction, I was able to get a lot done on evenings when I was otherwise too tired to program.
The project even ended up more sophisticated and polished as a result. I ended up with animations for game character movement that I would never have pursued had Gemini not made a quick almost-working initial implementation.
One of my biggest challenges with hobby projects is regaining momentum after a break. I found that using a coding agent like Gemini made it much easier to start and rebuild momentum after stalls. And it also prevented some stalls entirely: on nights I otherwise wouldn't have had time to do anything, I could write a quick prompt and end up with a patch for a task on the TODO list.
I found it vital to have unit test coverage. Gemini did a pretty good job adding coverage when I requested it. As test coverage became extensive, I was able to move quickly without breaking important game behaviors. It was great to enable Gemini to run unit tests using node to vet and fix new logic in a loop. Before using Gemini on this project, I had a backlog of tests I needed but didn't feel like writing. With Gemini, I had all of them written in a few evenings.
I approach Gemini with a high level of scrutiny: I run Gemini as a separate Linux user, with filesystem permissions only for the project directory. I review and approve every command it runs. I review and often edit every patch before committing it. This is working well for me.
Other useful tools:
- As usual, I used PCEImage Editor to create many graphics, including animation frames.
- I used Frank Force's tiny ZzFX library for sound effects. (backup)
- I am working on an LLM prompt to make it easy to create new Wolfers game variants. I hope to make a "create your own Wolfer" page where people can create a Wolfers game and submit it. I used the work-in-progress prompt to create Phonics Wolfer.
- Update: Create Your Own Wolfer is now live! (Details)
- Wolfers games look good on phones, iPads, and can also be installed as progressive web apps on your home screen. I recently found a simpler way to make PWAs thanks to this minimal-pwa project. I made this a bit more dynamic and self-contained in Wolfer's pwa.js and added offline PWA support in sw.js.
 Introducing Phonics Flashcards!
Introducing Phonics Flashcards!My 4-year-old son is learning the basics of reading, starting with the sounds of every alphabet letter.
A friend of ours recommended cardboard flashcards by toddlersread.com.
This company shared a few helpful videos on how to use phonics flashcards effectively and what sound to learn first for each letter.
The cards we like best are sold out so I made this web app to use in the meantime.
Key features:
- Focus on just a few letters at a time. When the page loads, the five letters with the weakest recall are chosen automatically. Tap into the Letters menu to customize which letters are in rotation in the current session.
- Show uppercase and lowercase letters together. These can usually be learned at the same time. If your kid needs to focus on one at a time, this can be customized in the settings panel.
- A fun image is behind the reveal instead of on the front of the card. We want kids to learn the sound based on the letter alone. We don't want them to memorize the sound based on a single image.
- When there's an "easy recall" streak, there's a fun confetti animation to keep kids engaged.
- Flashcards are chosen and sorted using a spaced repetition algorithm (the same one used in my Mandarin Flashcards). That's why there are three buttons (and swipe actions) to quickly indicate whether the flashcard was not-yet-known, slow to recall, or easy to recall. Not-yet-known and slow cards are shown more frequently until recall improves.
- This web app should look good on phones, iPads, and can also be installed as a PWA on your home screen.
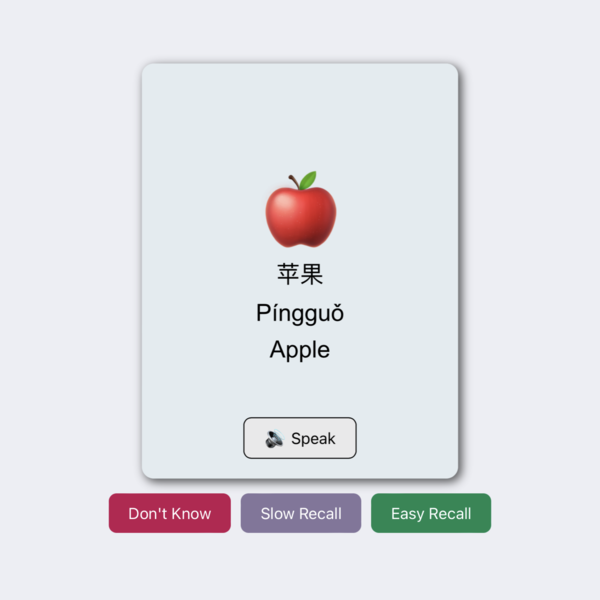 Introducing Mandarin Flashcards!
Introducing Mandarin Flashcards!I'm expanding on Mandarin Communication Board by using the same data to create a set of flashcards.
These flashcards use spaced repetition, a memorization method where cards you don't know yet will appear frequently and cards you know well will appear less often. This technique has been popularized by the Anki flashcards app.
When you review each card, you indicate whether you don't know it, you recalled it with effort, or it was easy to recall. The web app then calculates and schedules the next time it should be reviewed. Over time, well-known cards will be scheduled several days into the future.
With this technique, you can spend ~10 minutes a day reviewing cards to learn hundreds of words.
Some technical details:
- Learn more about its companion project's development details: About Mandarin Communication Board
- I reused almost everything from this project
- I implemented a swipe left/up/right UI that should feel great on iPhone. I find it a lot of fun to play with the cards!
- I originally tried to have ChatGPT implement the swipe UI. After several rounds of iteration, I had an 80% working implementation but it was so tangled that I started looking for another option. I found this great and simple codepen with no dependencies which I switched to as my starting point.
- Click the settings gear to see your learning statistics!
- Unmute your device and turn up the volume if you don't hear anything when clicking the "Speak" button
- This website can be added to your home screen as a PWA
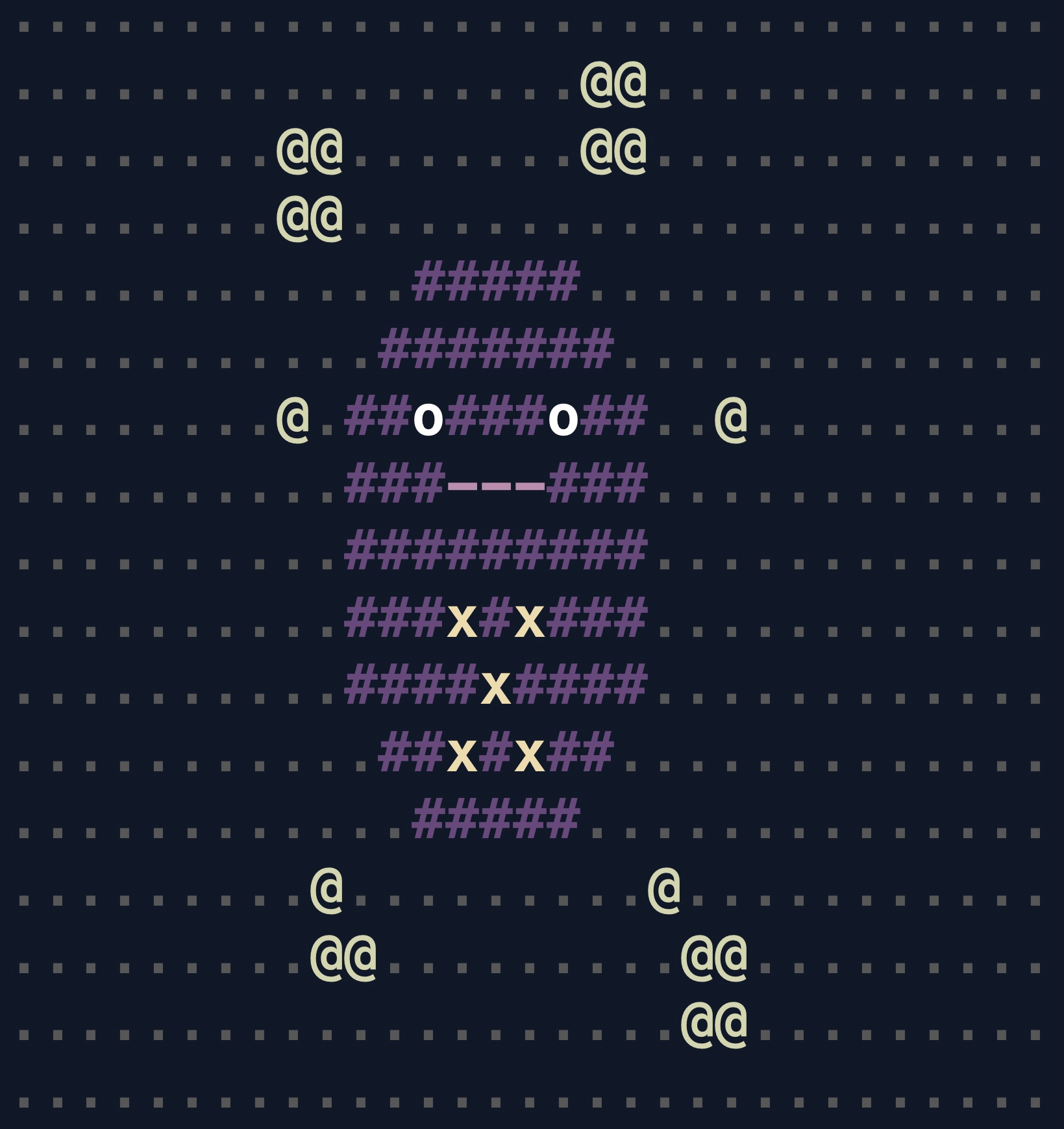
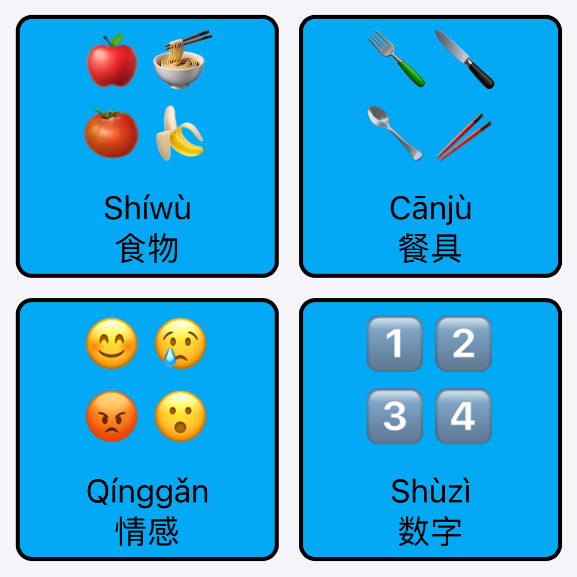 Happy Lunar New Year!
Happy Lunar New Year!Introducing the Mandarin Communication Board, a tool for learning and communicating in Mandarin Chinese.
My son recently started showing interest in learning Mandarin thanks to some singing books sent by a friend of ours.
I made this tool to help us expand our vocabulary and enable us to communicate about every day stuff.
My favorite part as I dabble in Mandarin is that there is no verb conjugation! Grammar tends to be fairly simple, too, which means that you can start saying intelligible sentences quickly by picking up common words.
The toughest part so far is hearing and producing words with the right tones. To my untrained American ears, I often can't tell the difference between words that differ only in their tone. It's been helpful to see the words written in pinyin and spoken aloud using this communication board.
Some technical details:
- I'm using the built-in SpeechSynthesis browser API, which produces audio that's good enough with the voices in Safari. I'm considering using higher quality TTS, like Google's, which appears to have a generous free tier.
- I used ChatGPT to do much of the hard work, including producing a lot of the vocabulary list. ChatGPT also contributed many of the word-to-emoji pairings. I had to remove many that were too abstract or a bad fit, though.
- For some words, I used iOS's new Genmoji feature to create images. I'm happy with the results!
- For other words, I used the wonderful and free images provided by ARASAAC. I found this organization by searching for "AAC images". AAC stands for "Augmentative and Alternative Communication".
- For a few words, I used Unsplash
- There are ~20 words and phrases with no images and I don't think I will find good ones for them
- I want to look into adding the full set of HSK1 and HSK2 vocabulary
- I am targeting Apple devices so it's likely that TTS or the full set of emoji may not show up on other operating systems
- This website can be added to your home screen as a PWA. I'm considering hooking it up to launch when I press the action button on my iPhone for quick reference.
- As a follow-on project, I might use this dataset to create flash cards to use with spaced repetition. Update: check out the flashcards project!
 Introducing Counting Tap Toy, the latest addition to the Tap Toy series.
Introducing Counting Tap Toy, the latest addition to the Tap Toy series.(See also: Slice Tap Toy, Fireworks Tap Toy, Tap Toy)
In Counting Tap Toy, you can tap to count various fish and aquatic creatures. The count is displayed and announced.
I built this game for my 3-year-old son. He's pretty good at counting with one exception: he always skips "14". My hope is that seeing and hearing the numbers will reinforce 14's existence and teach the pattern of the teens and beyond.
Some technical details:
- I whipped this game up in my spare hours during winter break after shipping Space Trader
- The count is announced using the SpeechSynthesis API
- Unlike the prior Tap Toys which use Matter.js, I picked LittleJS by Frank Force. I've admired Frank's work for a long time and I was dissatisfied with Matter.js's inconsistent behavior on devices with different screen refresh rates. I wasn't able to fix that to my satisfaction in Slice Tap Toy -- frame drops are still sometimes noticeable.
- I'm generally pleased with LittleJS in this project. The example projects gave much of what I needed and the engine provides a lot of cool stuff, including systems for creating sound effects and particle effects.
- I needed to hack in a few behavior changes which were tricky to achieve: a full-screen canvas, simultaneous mouse and touch support, direct callbacks for handling user input (since the SpeechSynthesis API seems to ignore calls without that direct tie to input), support for links overlaid on top of the game canvas. Fortunately, the code is straightforward and easy to modify.
- One quirk: image tiles had a weird "bleeding" glitch where I would sometimes see a sliver of the other side of the tile wrapping around. I saw that LittleJS has a hack to solve this (tileFixBleedScale), but that causes other visual glitchiness (to me, it made the tiles look like they were under water, slight stretching and shrinking as the game object moves around). I picked a different solution: having at least a few pixels of padding baked into the image assets.
- As usual, I used PCEImage Editor to create many graphics. I created the PCEImage format and tools so I could simply store and edit graphics as ASCII art. See them here.
- I got the image assets from someone who posted them with a permissive license on itch.io. Then I used PCEImage Editor to import and convert them.
- Music came from chosic.com. Credits for the songs I used.
 Introducing my latest game, playable right in your web browser: Space Trader
Introducing my latest game, playable right in your web browser: Space TraderIn Space Trader, you can trade goods, hunt bounties, amass a fortune, buy a moon and retire.
Space Trader can be saved to your home screen as a PWA (Progressive Web App).
Space Trader started as a game written by Pieter Spronck for Palm OS, released in 2002. Wikipedia page. Official website (mirror).
You can play the original on archive.org.
As one of my favorites, this game holds a special place in my heart. I played a ton in middle school and high school. This is the second port of the game I've made.
Like SFCave (recreated as CaveRibbon), I decided to recreate Space Trader as a web app to feed my nostalgia and give the game new life. I hope this version of Space Trader can survive long into the future thanks to the universal availability of web browsers and their devotion to compatibility.
Some technical details:
- As usual, I used PCEImage Editor to create many graphics. I created the PCEImage format and tools so I could simply store and edit graphics as ASCII art. See them here.
- To aid debugging and unit testing, I use a deterministic random number generator called GameRand. In debug mode, I can capture the random seed and log of every action taken in the game. Then I can replay that to reproduce a bug or create a test.
- I've written many unit / integration tests for Space Trader. See them here.
- Learn more about GameRand in the post for CaveRibbon.
- A major downside to this technique for testing is that tests become invalid if a bug fix (or a new feature) changes the amount of random numbers consumed. I ended up remaking many tests one or two times. This added a few days of extra work to the project.
- You can play the game with cheats and access the replay log on a special version of the game: cheats.html.
- I translated an existing implementation of this game to vanilla JavaScript using ChatGPT. I could translate ~300 lines at a time. I audited every line produced. This worked pretty well and saved me a huge amount of time compared to manually translating the code. This was a somewhat zen activity for me because it was mechanical; tedious but rewarding to see how quickly I could progress through the whole codebase. This was the kind of programming I could do after an exhausting day at work. Major differences/difficulties:
- The original code relies on integer math, but JavaScript uses float math. I needed to ensure all uses of numbers yielded an expected result. I ended up adding exhaustive runtime asserts and writing automated stress tests to catch problems.
- ChatGPT would sometimes produce inconsistent translations, especially for enum names. These could lurk, waiting to cause a crash at runtime. I hunted these with stress tests, manual tests, nearly exhaustive code coverage, and replayable game logs (which I turned into tests).
- Similarly, ChatGPT would inconsistently translate properties and their setters/getters. I left many awkward translations in place to save myself time, even though it makes the code worse.
- The UI needed to be tailored to the web. I ended up writing almost all new code for the UI.
- The original code had no tests. I wrote all new tests and a quick-and-dirty system for measuring code coverage. I even discovered several longstanding bugs in the original code.
- Before translating the whole codebase, I investigated using emscripten to reuse as much of the original C code as possible. I decided I wouldn't be satisfied with the result. There wasn't separation of UI and business logic that would have let me easily build new UI tailored to web. There were a lot of Palm OS platform-specific functions that would need to be replaced. I didn't want to struggle to change the existing code where it became necessary.
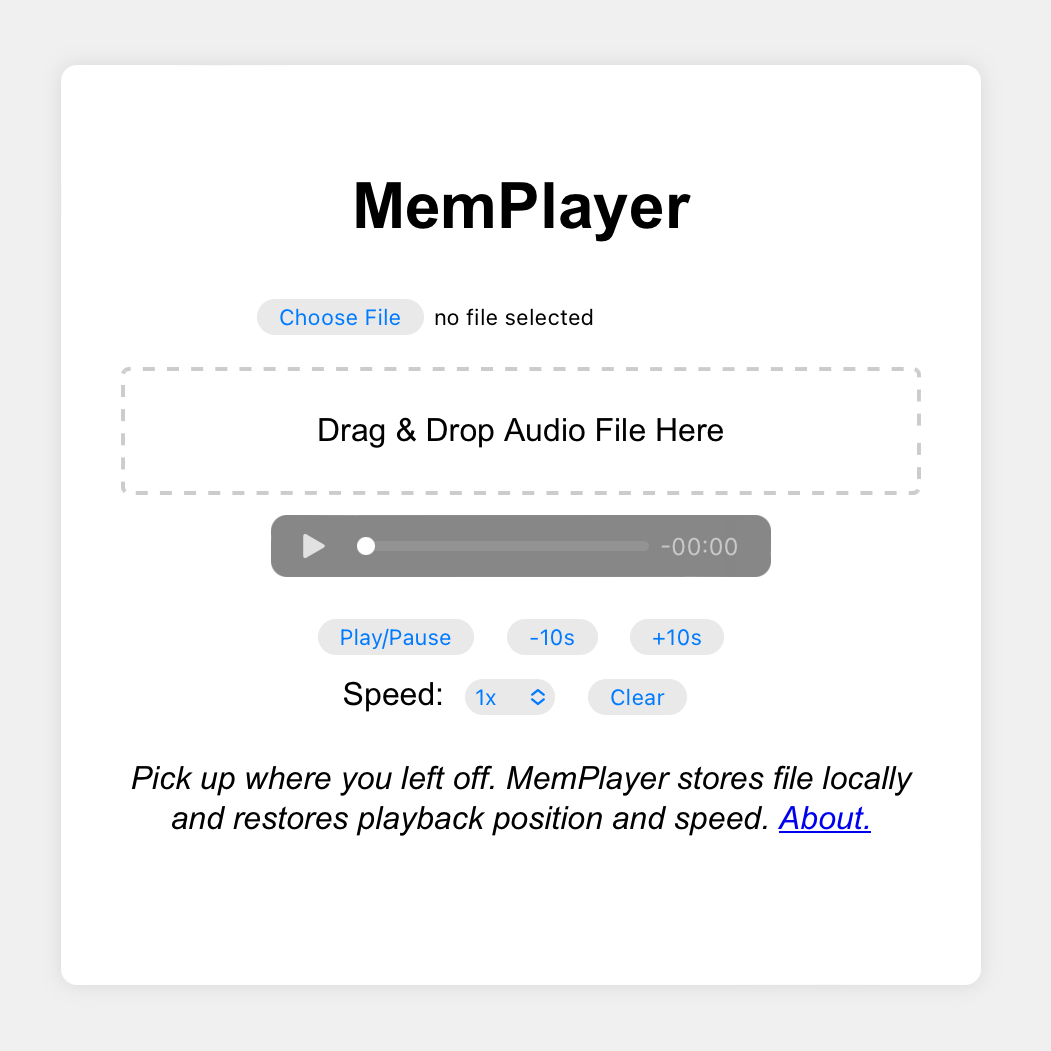 I recently whipped up a simple audio player dedicated to listening to long audio files across multiple listening sessions.
I recently whipped up a simple audio player dedicated to listening to long audio files across multiple listening sessions.It's called MemPlayer and you can try it here.
The problem MemPlayer solves:
I listen to most audiobooks in the excellent Libby app. It nails the core use case: remembers playback position, gives easy controls for jumping back/forward, and gives granular control over playback speed.
Sometimes, though, I have a book (or other long audio recording) as a single standalone audio file. I still need all of those features for easy listening across multiple days.
Instead of finding an existing app with exactly what I need, I experimented to see how quickly I could whip up a simple utility app using ChatGPT. I found the low overhead of web development plus ChatGPT to be a killer combination.
I started with this prompt:
Generate HTML, JavaScript, and CSS for a simple web app with these requirements:
- The user can browse their local disk to select an audio file
- Alternatively, the user can drag and drop an audio file onto the web app
- The web app allows the user to play the audio file, change playback speed, and skip forward and back by 10 seconds
- The web app stores the file in local storage and restores it when the page is refreshed
- The web app stores the current playback position and restores it when the page is refreshed. This way the user can load the page and resume what they were listening to.
- There is a clear button which causes the web app to forget the current audio file and playback position
This produced code for index.html, scripts.js, and styles.css that gave me 90% of what I needed. The UI was good, but the web app did not work perfectly.- The user can browse their local disk to select an audio file
- Alternatively, the user can drag and drop an audio file onto the web app
- The web app allows the user to play the audio file, change playback speed, and skip forward and back by 10 seconds
- The web app stores the file in local storage and restores it when the page is refreshed
- The web app stores the current playback position and restores it when the page is refreshed. This way the user can load the page and resume what they were listening to.
- There is a clear button which causes the web app to forget the current audio file and playback position
I steered it with a few specific suggestions in subsequent prompts, mainly to use IndexedDB to store the audio file because its original choice, localStorage, can't handle big files. I also needed to fix a bug in restoring playback position. I then made some minor style and user experience tweaks, added PWA metadata and icons, and was done!
Overall, I was able to whip this up in about an hour, with some of the fixes and tweaks done on the go.
I think there's a lot of potential to make custom tiny tool web apps with low effort this way. And one of the best parts of the web is that nearly everyone can use these tools without any setup across their phones, tablets, computers, etc. And they will hopefully continue working for decades to come without any developer intervention.
 Introducing my latest project, playable right in your web browser: Slice Tap Toy
Introducing my latest project, playable right in your web browser: Slice Tap ToySlice Tap Toy can also be saved to your home screen as a PWA (Progressive Web App).
This project is my spin on the touch screen swipe-to-slice concept. Every pizza can be sliced multiple times, down to tiny slivers. Can you unlock the whole menu?
Swiping across a touch screen to slice objects is a delightful and fun mechanic. You might remember some of the best early games for iPhone: Fruit Ninja and Cut The Rope.
Unfortunately, these formerly wonderful games are no longer delightful, now with constant interruptions and ads. Go try them and see for yourself. These games have been ruined.
Slice Tap Toy is a simple passion project so it can be light, fun, and pristine.
Development details:
I was inspired to make Slice Tap Toy when I came across Samurai Sam, an entry to the 2023 JS13KGames competition. This got me thinking about slicing games.
I decided to do some quick prototyping by hacking on Tap Toy's source code. I vetted that I could track slices from touch and mouse input, draw the slices, and detect collisions without much work. Like the original Tap Toy, I use PCEImage for the art.
Like CaveRibbon (project details), I used LLMs to help. I could do some things faster, I was able to get the website to look how I wanted without becoming an expert on CSS, and (new to this project) I was able to get artistic inspiration for the art. I asked DALL-E to generate pizza pixel art. What I got were grotesque abominations that, to this day, have eroded some of my enjoyment of pizza. I stared at flesh colored cheese and glitchy toppings and turned them into my own cleaner pixel art pizzas. I'll spare you the examples.
 Introducing my latest game, playable right in your web browser: CaveRibbon
Introducing my latest game, playable right in your web browser: CaveRibbonCaveRibbon is a one-button game where you control a ribbon gliding through a shrinking cavern. Avoid the walls and obstacles as long as you can. Compete with yourself and your friends by sharing a replay. Submit your high scores to get into the hall of fame!
CaveRibbon can be saved to your home screen as a PWA (Progressive Web App).
This game is a tribute to Sunflat's SFCave for Palm OS. You can play the original on archive.org.
In fact, it was archive.org that stirred up my nostalgia over a year ago by publishing a collection of 565 Palm OS apps, all usable on the web thanks to a Palm OS emulator.
When I was in middle school, I would play SFCave on a Palm m130 at night when I was supposed to go to bed. My dad and I had an ongoing competition to see who could get the highest score.
This was my inspiration to add the replay and share features which let you replay the exact same round, with your previous playthrough visible as a head-to-head competitor.
Some technical details:
- I used PCEImage Editor to create the pixel font and many graphics. I created the PCEImage format and tools so I could simply store and edit graphics as ASCII art. See them here.
- This game is entirely static files. There's no server-side backend. To create replay URLs, I need to serialize the entire game state into the URL itself. This proved to be challenging because there are URL size limits in browsers and messaging apps. In my first approach, I wrote a bunch of code to serialize all of the wall, obstacle, and player positions. This proved to be too much data. I came up with a few tricks to significantly shrink the data:
- I compress player positions lossily and then interpolate them as part of deserialization. I keep only positions at the top of a peak, bottom of a valley, and when the user is close to an obstacle. I only have to keep ~4% of the original data.
- I use a deterministic random number generator called GameRand. As long as I reuse the random number generator's seed and don't change the code to use random numbers differently I will get the exact same wall and obstacle positions in a replay.
- I first came across GameRand in phoboslab's game underrun (source).
- I searched for the constant 0x49616E42 to find the origins of this function. This led me down a rabbit hole: a StackOverflow post which links to a blog post (now only available on archive.org) which links to this post from 2002 introducing a faster rand function by Stephan Schaem, who appears to be the original author.
- I couldn't just serialize the replay as JSON. That's not nearly compact enough (every digit is stored as a character!). Instead, I packed raw bytes into a buffer and serialized that into Base64. I did some tweaks to squeeze some additional efficiency (such as replacing characters that need to be percent-encoded in URLs).
- Replay URLs for scores of 700 or higher get a nice image preview (Open Graph image) that includes the score. I generated all of these files statically using PCEImage and a script.
- This is the first project where I've made use of an LLM to help. I used ChatGPT and it had great positive impact:
- It helped me do some things faster, such as writing boilerplate or example code that I would have had to write myself while wading through documentation.
- It helped me do some things I wasn't willing to do myself. I don't have time to learn the right way to get specific UI behaviors using HTML and CSS. I would have compromised the UI design to fit within my current skills. With ChatGPT's help, I was able to get exactly what I wanted much faster than having to learn how to do this on my own.
- In general, I'm energized to work on more projects with these tools. I found the accuracy to be far above what I expected. It's more than good enough for a non-mission-critical side project.
- I'm trying out some design ideas from Bret Victor's Magic Ink paper (backup). My favorite insights:
- Most software design should focus on information graphic design, not interaction design
- The case study of Amazon's book listings drives that point home
- Try using sentences to describe settings rather than have a list of toggles (illustrated with his BART widget). I use this concept for sound effects settings in CaveRibbon.
- Instead of requiring interaction, make decisions for the user based on context. I use this idea in CaveRibbon by fading out the rest of the UI during gameplay instead of having a "full screen" button.
See also:
- Sunflat's latest games for iOS and Android

Posted on 12/23/2023
Tags: Games
In an HN post about a very cool PuzzleScript game called Enigmash, I learned sad news.Tags: Games
Jack Lance, the author of the game, died earlier this year.
I went to his website, jacklance.github.io, and saw that it had been updated to refer to him in the past tense.
Seeing that the site is hosted on GitHub, I looked at the recent updates. I discovered two things:
- He made this update himself, to show up a few days later
- He published one last game, Octogram, but unfortunately made a typo in the URL to the game
- Update 12/30/23: I commented on the git commit and one of Jack's siblings saw it. They pushed a fix and now the link on Jack's website is working!
Here's a working link to Jack Lance's last game: Octogram.
It's a super tricky puzzle game with fun wordplay. Give the source code a peek if you get stuck -- but beware this will spoil all of the answers!
More resources:
- Jack's games
- Jack Lance on Puzzle Wiki
- A blog post about Jack's work
- Another blog post about Jack's work
- Backup of jacklance.github.io
- Due to some technical details of PuzzleScript, none of his PuzzleScript games are in this repo. Instead, they are stored as GitHub gists. I've grabbed a separate backup of every gist linked to by his games page for posterity.
- A YouTube video where Jonathan Blow mentions Jack's death. "...he was 25... he was already one of the best game designers in the world and was on track to be even better"
- Obituary under his real name
Posted on 11/27/2023
Tags: Programming
In the same vein as FreshRSS, another open source project with a cool API is Mastodon.Tags: Programming
Many users I followed on Twitter (now X) have migrated to Mastodon. I found that the Mastodon apps I tried didn't perfect the one thing I want: to read a chronological timeline of posts and reblogs from the accounts I follow - always keeping my spot since the last time I checked.
I had already written my own Twitter client for this, which I've been using for many years, and just finished adapting that for Mastodon.
The Mastodon API made this really easy! I can tell that a lot of care went into making this core use case straightforward. Thank you Mastodon developers!
Here's the short list of requests needed to make a simple Mastodon timeline viewer app:
Below, I'm using https://mstdn.party but you should substitute the Mastodon server you use.
1. Register your app.
- Docs: https://docs.joinmastodon.org/methods/apps/#create
- Replace YOURAPPNAME and YOURWEBSITE below. YOURWEBSITE should be a full url starting with "https://"
curl -X POST -F 'client_name=YOURAPPNAME' -F 'redirect_uris=urn:ietf:wg:oauth:2.0:oob' -F 'website=YOURWEBSITE' https://mstdn.party/api/v1/apps
The response is JSON and includes important fields you will need in later steps: client_id and client_secret. I'll refer to these as YOURCLIENTID and YOURCLIENTSECRET below.
2. Give your app permission to read your account information. Open this URL in your browser and authorize it. You'll be shown an authorization code which I'll refer to as YOURAUTHCODE below.
- Docs: https://docs.joinmastodon.org/methods/oauth/#authorize
https://mstdn.party/oauth/authorize?response_type=code&client_id=YOURCLIENTID&redirect_uri=urn:ietf:wg:oauth:2.0:oob
3. Get an access token for your app to use to request your account's timeline (and make any other helpful API requests).
- Docs: https://docs.joinmastodon.org/methods/oauth/#token
curl -X POST \
-F 'client_id=YOURCLIENTID' \
-F 'client_secret=YOURCLIENTSECRET' \
-F 'redirect_uri=urn:ietf:wg:oauth:2.0:oob' \
-F 'grant_type=authorization_code' \
-F 'code=YOURAUTHCODE' \
-F 'scope=read' \
https://mstdn.party/oauth/token
The response is JSON and includes the access_token. I'll refer to that as YOURACCESSTOKEN below.
4. Now your app can load your timeline.
- Docs: https://docs.joinmastodon.org/methods/timelines/#home
curl 'https://mstdn.party/api/v1/timelines/home' -H 'Authorization: Bearer YOURACCESSTOKEN'
The result is JSON with everything you need to display the timeline in full. I love that it's all included in a single API request! This even includes account information (display name, username, the image URL for the poster's avatar, and more) for the people you follow and the people whose posts they have reblogged.
One helpful argument to include is "limit". I like to request the max number of posts supported by the API, 40.
curl 'https://mstdn.party/api/v1/timelines/home?limit=40' -H 'Authorization: Bearer YOURACCESSTOKEN'
When refreshing my app, I want to request all posts that are new since the last time I refreshed. I accomplish this by using the max_id argument.
I start by requesting the most recent 40 posts:
curl 'https://mstdn.party/api/v1/timelines/home?limit=40' -H 'Authorization: Bearer YOURACCESSTOKEN'
I check if this includes the last post my app is aware of. If not, I request farther back by including "max_id=" the id of the oldest post in the response I just got. Example:
curl 'https://mstdn.party/api/v1/timelines/home?limit=40&max_id=123456789' -H 'Authorization: Bearer YOURACCESSTOKEN'
I continue loading back like this until any of these conditions are true:
- I find posts that my app already knows about
- I get no posts in response
- I get posts older than 1 month (I don't want to accidentally load back too far)
- I've made more than 5 requests (I don't want to create excess traffic)
And that's it! My app only needs to use a single API to refresh my timeline. I did steps 1 through 3 manually and hard-coded the access token into my app, using it to perform step 4 every time I want to refresh. This is ok because this app is just for me so I don't need a more dynamic authentication flow.1. Register your app.
- Docs: https://docs.joinmastodon.org/methods/apps/#create
- Replace YOURAPPNAME and YOURWEBSITE below. YOURWEBSITE should be a full url starting with "https://"
curl -X POST -F 'client_name=YOURAPPNAME' -F 'redirect_uris=urn:ietf:wg:oauth:2.0:oob' -F 'website=YOURWEBSITE' https://mstdn.party/api/v1/apps
The response is JSON and includes important fields you will need in later steps: client_id and client_secret. I'll refer to these as YOURCLIENTID and YOURCLIENTSECRET below.
2. Give your app permission to read your account information. Open this URL in your browser and authorize it. You'll be shown an authorization code which I'll refer to as YOURAUTHCODE below.
- Docs: https://docs.joinmastodon.org/methods/oauth/#authorize
https://mstdn.party/oauth/authorize?response_type=code&client_id=YOURCLIENTID&redirect_uri=urn:ietf:wg:oauth:2.0:oob
3. Get an access token for your app to use to request your account's timeline (and make any other helpful API requests).
- Docs: https://docs.joinmastodon.org/methods/oauth/#token
curl -X POST \
-F 'client_id=YOURCLIENTID' \
-F 'client_secret=YOURCLIENTSECRET' \
-F 'redirect_uri=urn:ietf:wg:oauth:2.0:oob' \
-F 'grant_type=authorization_code' \
-F 'code=YOURAUTHCODE' \
-F 'scope=read' \
https://mstdn.party/oauth/token
The response is JSON and includes the access_token. I'll refer to that as YOURACCESSTOKEN below.
4. Now your app can load your timeline.
- Docs: https://docs.joinmastodon.org/methods/timelines/#home
curl 'https://mstdn.party/api/v1/timelines/home' -H 'Authorization: Bearer YOURACCESSTOKEN'
The result is JSON with everything you need to display the timeline in full. I love that it's all included in a single API request! This even includes account information (display name, username, the image URL for the poster's avatar, and more) for the people you follow and the people whose posts they have reblogged.
One helpful argument to include is "limit". I like to request the max number of posts supported by the API, 40.
curl 'https://mstdn.party/api/v1/timelines/home?limit=40' -H 'Authorization: Bearer YOURACCESSTOKEN'
When refreshing my app, I want to request all posts that are new since the last time I refreshed. I accomplish this by using the max_id argument.
I start by requesting the most recent 40 posts:
curl 'https://mstdn.party/api/v1/timelines/home?limit=40' -H 'Authorization: Bearer YOURACCESSTOKEN'
I check if this includes the last post my app is aware of. If not, I request farther back by including "max_id=" the id of the oldest post in the response I just got. Example:
curl 'https://mstdn.party/api/v1/timelines/home?limit=40&max_id=123456789' -H 'Authorization: Bearer YOURACCESSTOKEN'
I continue loading back like this until any of these conditions are true:
- I find posts that my app already knows about
- I get no posts in response
- I get posts older than 1 month (I don't want to accidentally load back too far)
- I've made more than 5 requests (I don't want to create excess traffic)
 There's not enough time in the day for everything I want and need to do. Parenting, work, exercise, hobbies, sleep, etc.
There's not enough time in the day for everything I want and need to do. Parenting, work, exercise, hobbies, sleep, etc.I've found that even optimizing a few minutes here and there can add up to make life easier and more enjoyable. I still use tools for consuming text and audio/video faster.
Here's one of the biggest new optimizations I was able to make this year.
I had a bunch of work time and a bunch of hobby time I wanted to spend in front of a keyboard. This is thoughtful writing or programming time that couldn't be stolen a few minutes at a time while waiting in line, walking between meetings, etc.
I also had a bunch of underutilized time on a stationary exercise bike. I mostly spent that time reading news feeds or watching TV/movies. I enjoyed that a lot, but it wasn't the right balance of time spent doing that when I had other things I wanted to prioritize.
I searched for a product that would let me use a laptop or iPad + keyboard case while exercising on the stationary bike.
I came across airdesks.com and bought their laptop desk. I got the 64" tall, "Average Size Laptop", No AirShelves config. It's been awesome. I use it on the bike every day and occasionally as a standing desk.
Right now, I'm writing this post while exercising on the bike while my son is napping -- something I couldn't have squeezed in without this desk!
More posts:
FreshRSS
Fireworks Tap Toy
Remember Forgotten Names
Emscripten on Raspberry Pi 400
Simplify Picking a Restaurant
Trippy Art
Tap Toy
PCEImage Editor
PCEImage
My Beatles Picks
SoundsJustLike
PuzzleScript
Wheat Chex
PICO-8
Fussy Baby Checklist
Fall Asleep
Shape Your Destiny
Tim's Vermeer
Day and Night
Lights Off
Batman Curve
FormulaGraph
Bouncing Ball
Catalog of Math Shapes
Draw Shapes Using Math
Similar Songs
Building a Reddit app
Counterfeit Monkey
Listed Action Interactive Fiction
Andrew Plotkin's Zarfhome
Product Review Writing Prompts
Dungeon Memalign
Pac-Man Dungeon
The Queen's Gambit
Rebecca Meyer
Coding Machines
Clamps
Emoji Simulator
Universal Paperclips
Fall Down the Rabbit Hole
Live COVID-19 Dashboard
Create COVID-19 Graphs Using JavaScript
Books
notes.txt
Download Video Into Your Brain
Download Text Into Your Brain
Source Control
Personal Projects
How to Program a Text Adventure
RSS and Feedly
Welcome