I enjoy drawing shapes using math. Much of the fun is exploring what formulas look like and figuring out how to warp them to look different.

To be able to build more complex shapes and animations, in this post I'll explore some formulas and create a catalog of shapes.


Circles:

x^2 + y^2 = 1

Graphtoy requires that we solve for y to create a function of x: f(x)

y^2 = 1 - x^2
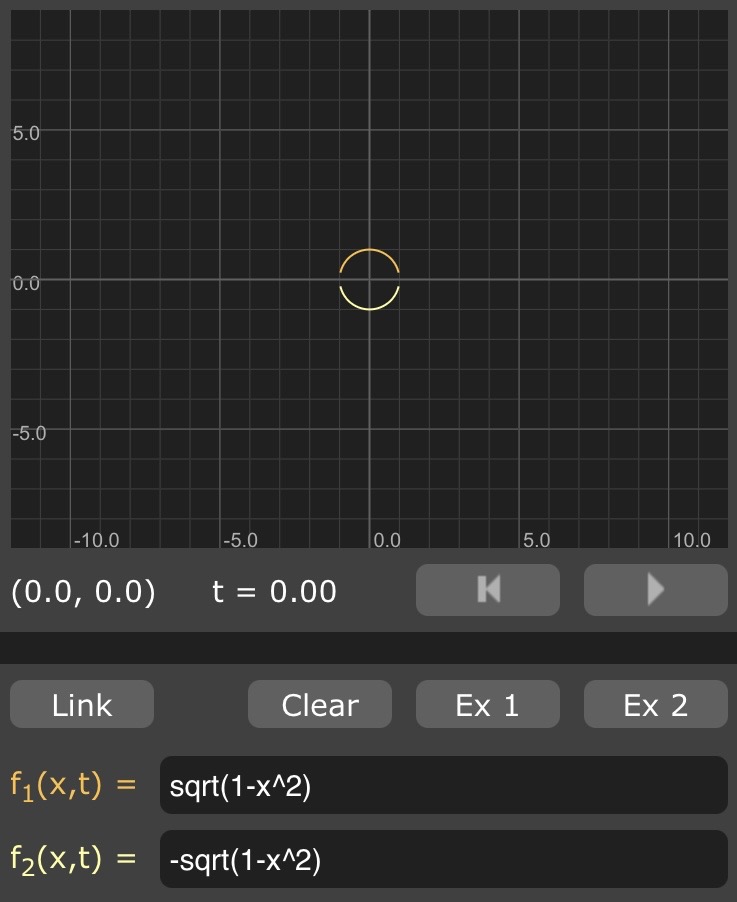
y = ± sqrt(1 - x^2)
f(x) = y = ± sqrt(1 - x^2)


Graphtoy doesn't understand ± so we need to write two separate formulas:
y = sqrt(1 - x^2)
y = -sqrt(1 - x^2)
Graphtoy link

Here's what that looks like:


In general, we can shift formulas up/down by adding/subtracting to/from the function. Here, we shift the circle up the y-axis by 2:
y = sqrt(1 - x^2) + 2
y = -sqrt(1 - x^2) + 2
Graphtoy link

And we can shift left/right similarly by adding/subtracting from every instance of "x". Here, we shift the circle left on the x-axis by 3:

y = sqrt(1 - (x+3)^2)
y = -sqrt(1 - (x+3)^2)
Graphtoy link

We can combine these two techniques to shift left and up at the same time:

y = sqrt(1 - (x+3)^2) + 2
y = -sqrt(1 - (x+3)^2) + 2
Graphtoy link


Lines:

y = mx + b
m is the slope (change in y divided by change in x)
b is the y-intercept (notice that adding b is the same technique we used to shift the circle up)

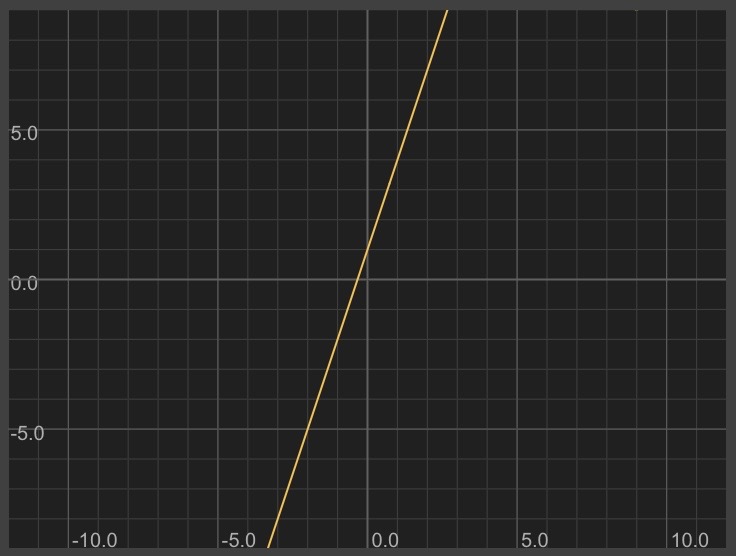
Here's a steep line that goes up 3 in the y direction for every increase of 1 in the x direction. I shifted it to intersect with the y-axis at y=1

y = 3*x + 1
Graphtoy link

Here's what that looks like:


In general, we can flip the shape over the x-axis by making it negative (notice this is similar to the way we draw the bottom half of a circle, by flipping the formula to the top half):

y = - (3*x + 1)
Graphtoy link

Similarly, we can flip a shape over the y-axis by replacing every instance of "x" with "-x":

y = 3*(-x) + 1
Graphtoy link


Sine wave:

y = sin(x)
Graphtoy link

Here's what that looks like:


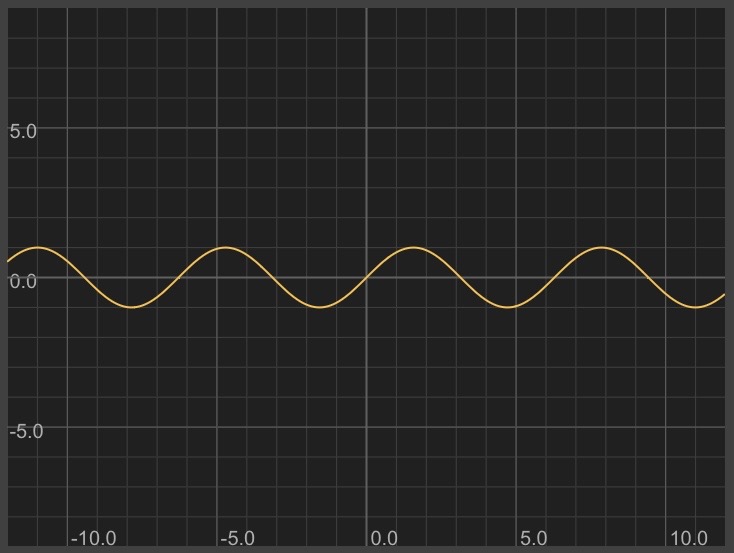
Something special about the shape of sin(x): it's periodic, repeating infinitely.


Parabola:

y = x^2
Graphtoy link

Here's what that looks like:


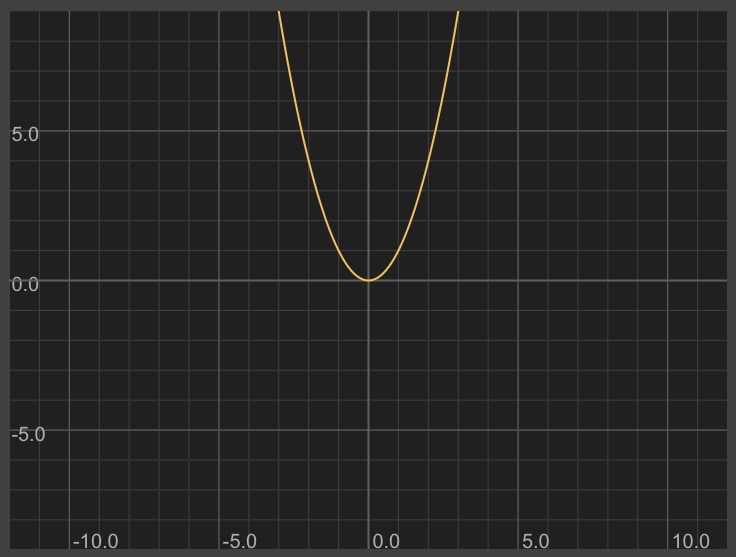
If we want to turn a shape sideways (by swapping the axes), we can swap x and y.

Sideways parabola:

x = y^2

Solve for y to be able to graph using Graphtoy:

y = ± sqrt(x)

y = sqrt(x)
y = -sqrt(x)
Graphtoy link


Combining shapes:

We can combine formulas to combine their shapes. For example, we can make a sine wave follow the shape of a line by adding them together:

Diagonal line:
y = x + 3

Sine wave:
y = sin(3*x)

Diagonal sine wave:
y = x + 3 + sin(3*x)
Graphtoy link


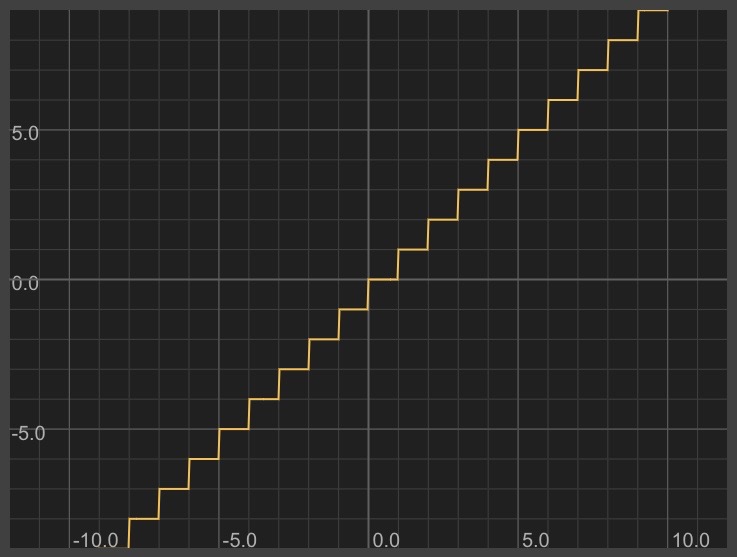
Steps (floor):

We can do some neat things using functions like floor and ceil. Floor rounds down to the nearest integer. Ceil rounds up to the nearest integer.

y = floor(x)
Graphtoy link

This looks like steps!


We can make a spiky sawtooth wave by only giving y the decimal portion of x like this:
y = x - floor(x)
Graphtoy link

To get an intuitive understanding of a shape, sometimes it helps to write out some of the values in a table:
This hopefully makes it easier to see how this ends up looking like a sawtooth.


Triangle wave:

I noticed that I might be able to construct a triangle wave by combining a sawtooth wave with a flipped sawtooth wave.

The naive approach of simply adding them together gives us this:
Sawtooth wave:
y = x - floor(x)
Flipped (across the y-axis) sawtooth wave:
y = -x - floor(-x)
(Note: when writing this, I accidentally flipped the formula over the x-axis: y = -(x-floor(x)). When I graphed it, I realized my mistake and played around with the -s to get it right. It's normal to play around and make mistakes! Make some terms negative and see what happens to the shape!)

Added together:
y = x - floor(x) + -x - floor(-x)
Graphtoy link

Ah woops! That looks like a straight line. Graphing the sawtooth waves on top of each other reveals why: the diagonal portions cross each other, summing up to a constant value for most values of x.
Graphtoy link

To get a triangle wave, I need to alternate taking a tooth from each sawtooth wave. I can take a tooth from one wave when floor(x) is even; a tooth from the other wave when floor(x) is odd.

That sounds pretty crazy! Fortunately, modular division is an easy way to test whether a number is even or odd.

Our gadget to determine when floor(x) is odd: mod(floor(x), 2)
We can use that to make a complementary gadget to determine when floor(x) is even: 1-mod(floor(x), 2)

Sawtooth wave:
y = x - floor(x)

Flipped (across the y-axis) sawtooth wave:
y = -x - floor(-x)

Using our gadgets to zero out every other tooth:

Graphtoy link

Here's what that looks like:


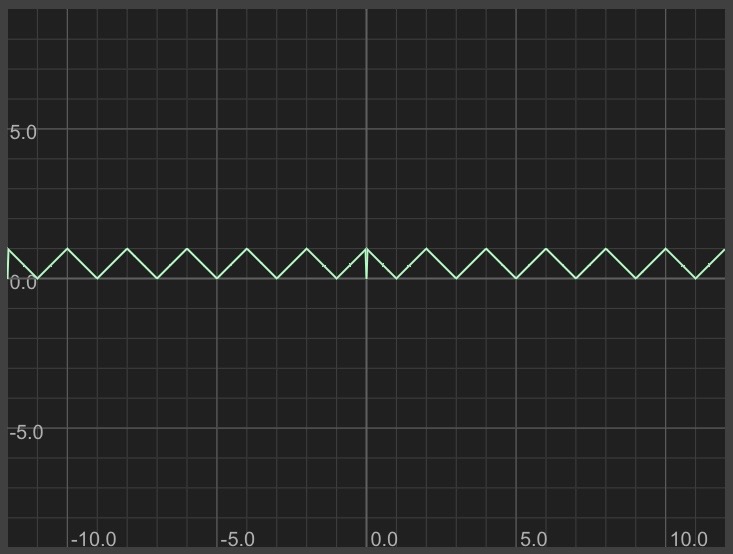
Notice that there are some visible glitches. Let's check the math:

y = mod(floor(x), 2) * (x-floor(x)) + (1-mod(floor(x), 2)) * (-x-floor(-x)))

Plug in x = 0:

y = mod(floor(0), 2) * (0-floor(0)) + (1-mod(floor(0), 2)) * (-0-floor(-0)))
y = 0 * (0-floor(0)) + (1-0) * (-0-floor(-0)))
y = 0

Ah but y is supposed to be 1. It looks like the equation has a bug.

Checking a few more x, y values to build intuition:
In its current form, our formula is taking neither sawtooth's value when x is a perfect integer (looking at the formula, you can see that it's because (x-floor(x)) and (-x-floor(-x)) are always 0 when x is an integer.

One fix is to add a term to our formula that has the value 1 for even integers and 0 otherwise.

I played around and came up with this:
(1-mod(floor(x),2))*(1-ceil(x-floor(x)))

The first half of this is our even/odd gadget. The second half is an expression that is 1 for integers, 0 otherwise.

Checking its values:
Fixed equation by adding this gadget:

y = (mod(floor(x),2))*(x-floor(x))+(1-mod(floor(x),2))*(-x-floor(-x)) + (1-mod(floor(x),2))*(1-ceil(x-floor(x)))
Graphtoy link

Here's what the fixed equation looks like:


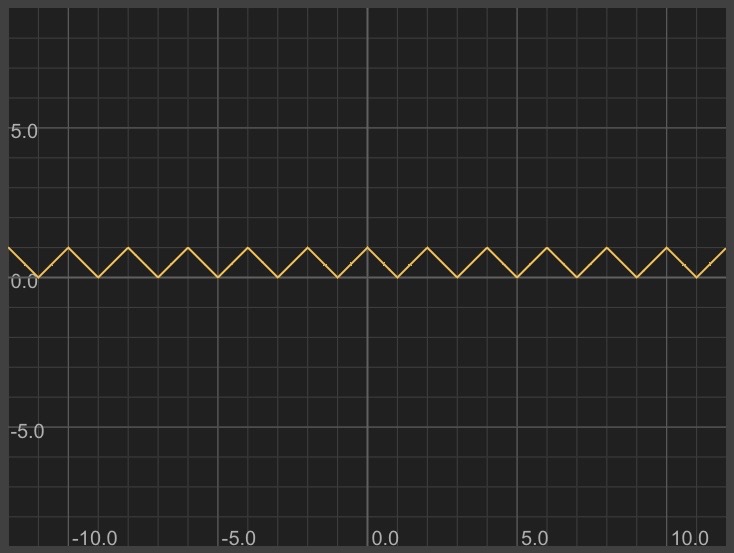
Looks perfect! Our formula is pretty complex, though. It's possible we could come up with a simpler formula by reading this Wikipedia page.


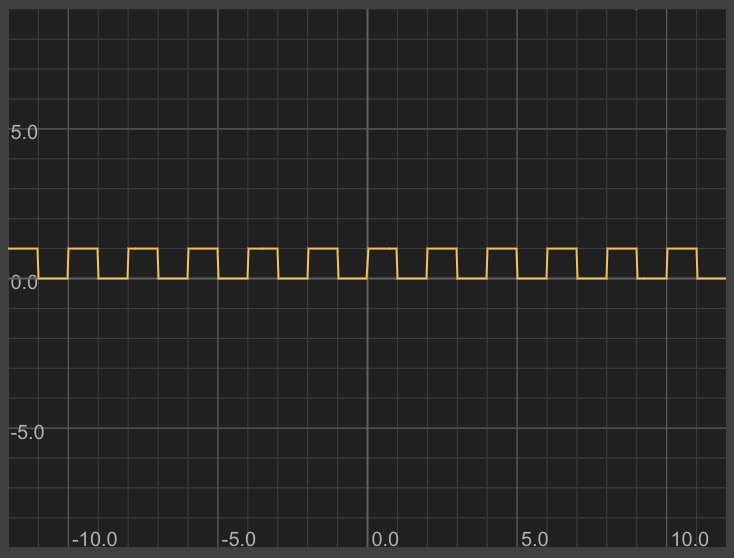
Square wave:

Here's one way to make a square wave: take an already periodic formula and make it blocky.

An easy periodic formula is sin(x).

y = sin(x)

Instead of having the period of sin be 2*PI, I can change it to be 2:

y = sin(x*PI)

I can use the "sign" function to turn positive values into 1 and negative values into -1:

y = sign(sin(x*PI))

If I want it to be truly square (1 tall and 1 wide), I'll need to adjust the height and shift it up:

y = sign(sin(x*PI))/2 + 0.5
Graphtoy link

Here's what that looks like:



How did I come up with these formulas and techniques? I remember many of these from school and others I (re)discovered by playing around. You can expand your own catalog by trying out new formulas to see what they look like and taking notes!

Here's a list of interesting things to explore:
log(x)
exp(x)
abs(x)
pow(x, n)
This animation that is built into Graphtoy
Growing concentric circles
Bouncing ball animation
Inigo Quilez's Useful Little Functions (my backup)